|
Hoofdstuk 5 Herstel van een oude wetenschap
Aan de andere kant van het hedendaags wetenschappelijk spectrum wordt een oude wetenschap hersteld. Eeuwenlang is ze angstvallig bewaard gebleven. Het is min of meer een kunstvorm en wordt de ‘Heilige Geometrie’ genoemd. Waarom heilig, wat is er zo heilig aan geometrie? In spirituele mysteriescholen uit het verleden werd onderwezen dat de Heilige Geometrie door God gebruikt werd om het universum te creëren. We weten inmiddels dat de Heilige Geometrie vele mysterieuze elementen bevat die op elegante wijze veel fenomenen beschrijft, zoals de groei van planten, de proporties van het menselijke lichaam, de omlooptijden van de planeten, licht, de structuur van kristallen, muziek, etc. De lijst gaat maar door. We zullen hiervan in dit hoofdstuk een aantal voorbeelden geven.
Waarom zouden we Heilige Geometrie introduceren in een boek dat handelt over hedendaagse vernieuwende wetenschap? De reden daarvoor is dat de Heilige Geometrie een sleutelrol lijkt te vervullen in een nieuwe, in opkomst zijnde postkwantumfysica. Deze nieuwe fysica lijkt beter in staat lijkt te zijn om het nulpuntsveld te verklaren en is een heropleving van de 19e eeuwse etherfysica.
De archaïsche wetenschap van de Heilige Geometrie kunnen we terugvoeren naar de Egyptische beschaving, maar het zou wel eens het erfgoed kunnen zijn van de beschaving van het mythologische Atlantis. We zullen in dit boek voldoende aanwijzingen aanvoeren om deze bewering te onderbouwen. Heilige Geometrie bevat elementen die cruciaal zijn om de etherfysica, die geïntroduceerd wordt in het volgende hoofdstuk, te kunnen begrijpen.
Verbazingwekkend genoeg is de Heilige Geometrie ook terug te vinden in de vele graancirkels die gedurende de laatste twee decennia over de hele wereld verschenen zijn. Het lijkt erop of iemand ons ergens betekenisvolle lessen leert. Ik zal niet ingaan op de oorsprong van deze graancirkels en erover speculeren of ze wel of niet van buitenaardse afkomst zijn, hoewel ik persoonlijk denk van wel. Dit valt (vooralsnog) toch niet te bewijzen.
Veel interessanter is eigenlijk dat de graancirkels intelligente ingebouwde geometrie vertonen. Feit is dat er ieder jaar wereldwijd honderden, ja zelfs duizenden van deze graancirkels verschijnen en dat hun ontwerp van een veel hogere intelligentie getuigt dan van de mensen die het mogelijk interessant genoeg vonden om ze na te maken.
Er is inmiddels voldoende bewijs dat, los van de graancirkels die inderdaad als nep zijn geïdentificeerd, de meerderheid van de graancirkels wel degelijk echt zijn. Zo is bewezen dat de stam van de gewassen op een vreemde manier gebogen is door een intense hitte, geproduceerd door een tot op heden onbekende energiebron, omdat de stam geen enkel brandmerk bevat. Daarnaast zijn er sterke energievelden gemeten in en om de graancirkels, vele uren nadat deze gevormd werden.
Volgens mij vormen deze graancirkels een hint voor onze hedendaagse wetenschappers om meer inzicht te verwerven in de betekenis van geometrie in de fysica in het algemeen en in het nulpuntsveld in het bijzonder.
In de oude leerscholen van de Heilige Geometrie meende men dat de heiligheid van het universum beschreven kon worden in termen van geometrische patronen van de hand van God. Hoe ongelooflijk dit ook mag lijken, middels veel voorbeelden is aantoonbaar dat veel onverwachte zaken een verborgen geometrie bevatten die op het eerste gezicht niet voor de hand ligt.
Men neemt nu aan dat de Egyptenaren de Heilige Geometrie toegepast hebben in de constructie van de Grote Piramide en veel andere monumenten. De Egyptenaren kenden twee mysteriescholen waarvan er een het Linkeroog van Horus genoemd werd. Deze school onderwees de vrouwelijk principes van de schepping, liefde en compassie. De andere school werd het rechteroog van Horus genoemd en hier onderwees men de intelligente mannelijk principes van de schepping; Heilige Geometrie was hier een hoofdvak.
De Heilige Geometrie heeft ook zijn sporen nagelaten in andere culturen zoals in de Gotische architectuur van Europese kerken en kathedralen (Chartres), het Parthenon in Athene, schilderijen van Leonardo Da Vinci en de hindoeïstische klassieke dans. In uiterste geheimhouding is de Heilige Geometrie ook gekoesterd door de vrijmetselaars.
(1)

Vrijmetselaars symbool
Het vrijmetselaarssymbool bestaat uit een winkelhaak en een passer; het zijn de enige twee instrumenten die nodig zijn om Heilige Geometrie te bedrijven. De gulden regel is dat wanneer je enig ander instrument dan deze twee nodig hebt om te bewijzen dat het met geometrie te maken heeft, dat het dan wel geometrie mag heten, maar zeker geen Heilige Geometrie!
Dankzij mensen als Robert Lawlor, Bruce Rawles en Drunvalo Melchizedek wordt de kunst van de Heilige Geometrie in ere hersteld en dankzij het enorme succes van het boek de ‘Da Vinci Code’ van Dan Brown dat populair werd in het jaar 2004, is het bewustzijn bij het grote publiek dat er kennelijk door de geschiedenis heen belangrijke informatie in het geheim bewaard is gebleven, toegenomen.
Laten we dan maar eens een snelcursus doen in deze heilige kunstvorm. En aan het slot beloof ik u een aantal verbazingwekkende dingen te laten zien.
De Levensbloem
Welnu, dit is een zeer belangrijk figuur in de Heilige Geometrie

Genesis patroon
Het wordt het genesispatroon genoemd. Onthoudt dat wat we hier zien in feite een tweedimensionale representatie is van wat in werkelijkheid driedimensionale bollen zijn! Afgebeeld in het plaatje ziet u ook een hexagram dat gevormd wordt door twee gelijkbenige driehoeken, het is het joodse symbool dat beter bekend is als de Davidster. De Davidster in dit plaatje is in werkelijkheid een driedimensionale stertetraëder. Hij bestaat uit twee in elkaar gevlochten piramiden, eentje naar boven wijzend en eentje naar beneden wijzend. Als u op zoek bent naar een voorbeeld van een stertetraëder, bekijk dan de omslag van dit boek eens.
Het volgende scheppingsverhaal werd onderwezen in de mysterieschool van het ‘rechteroog van Horus’ en vormde ook de basis voor de hermetische traditie (de wijsheid van Hermes Trismegistus alias de Egyptenaar Toth). Dit scheppings-verhaal ging waarschijnlijk ook rond in de vrijmetselarij.
In het begin schiep de universele geest van God vanuit het niets het brandpunt van het Godbewustzijn een enkele centrale bol. God was geheel en al omgeven door deze eerste bol op de eerste dag van de schepping. De volgende dag schiep God nog een bol, waarbij het centrum van deze tweede bol gelegen was ergens op het oppervlak van de eerste bol. De intersectie van deze twee bollen wordt de Vesica Pisces genoemd.
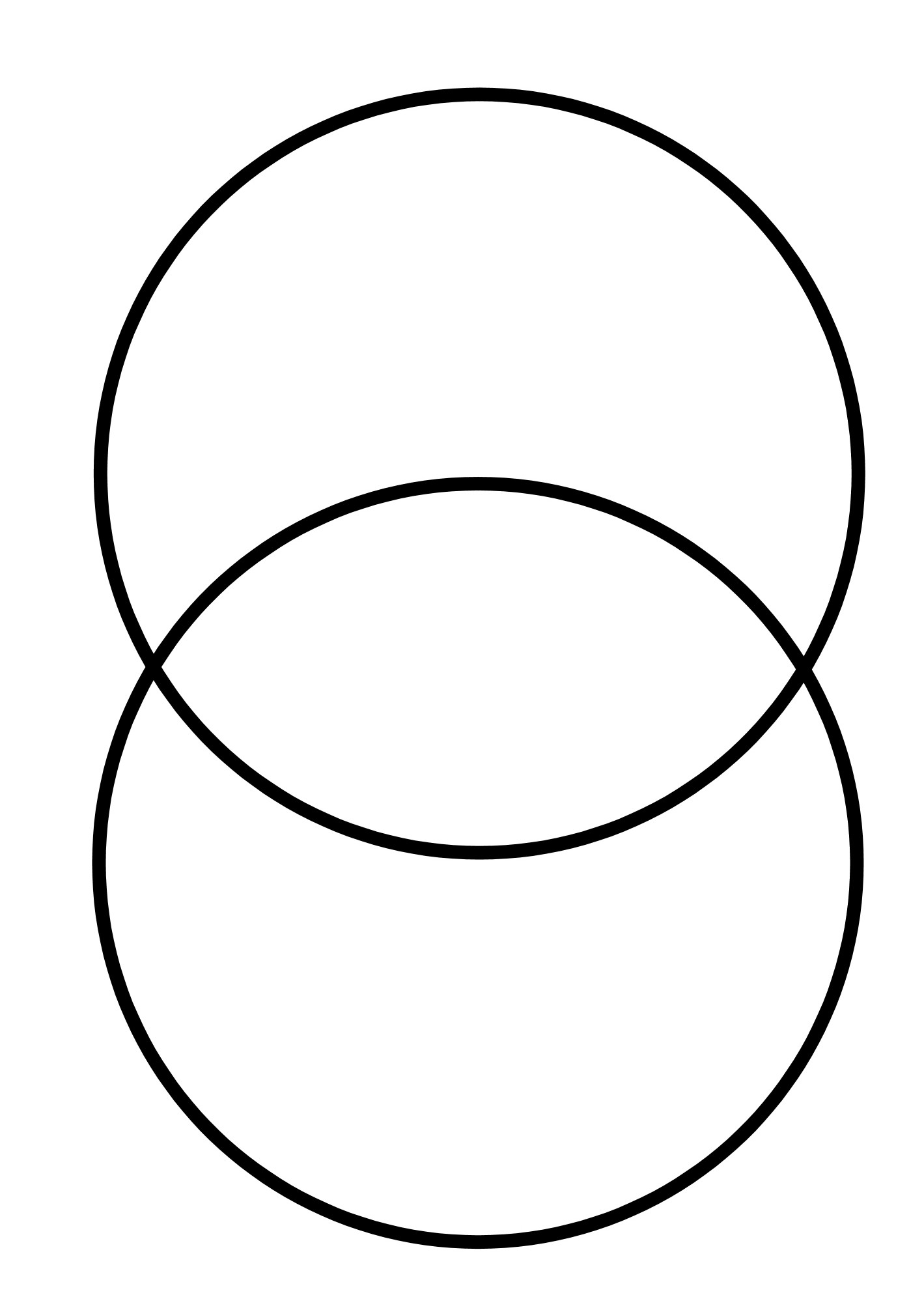
|
|
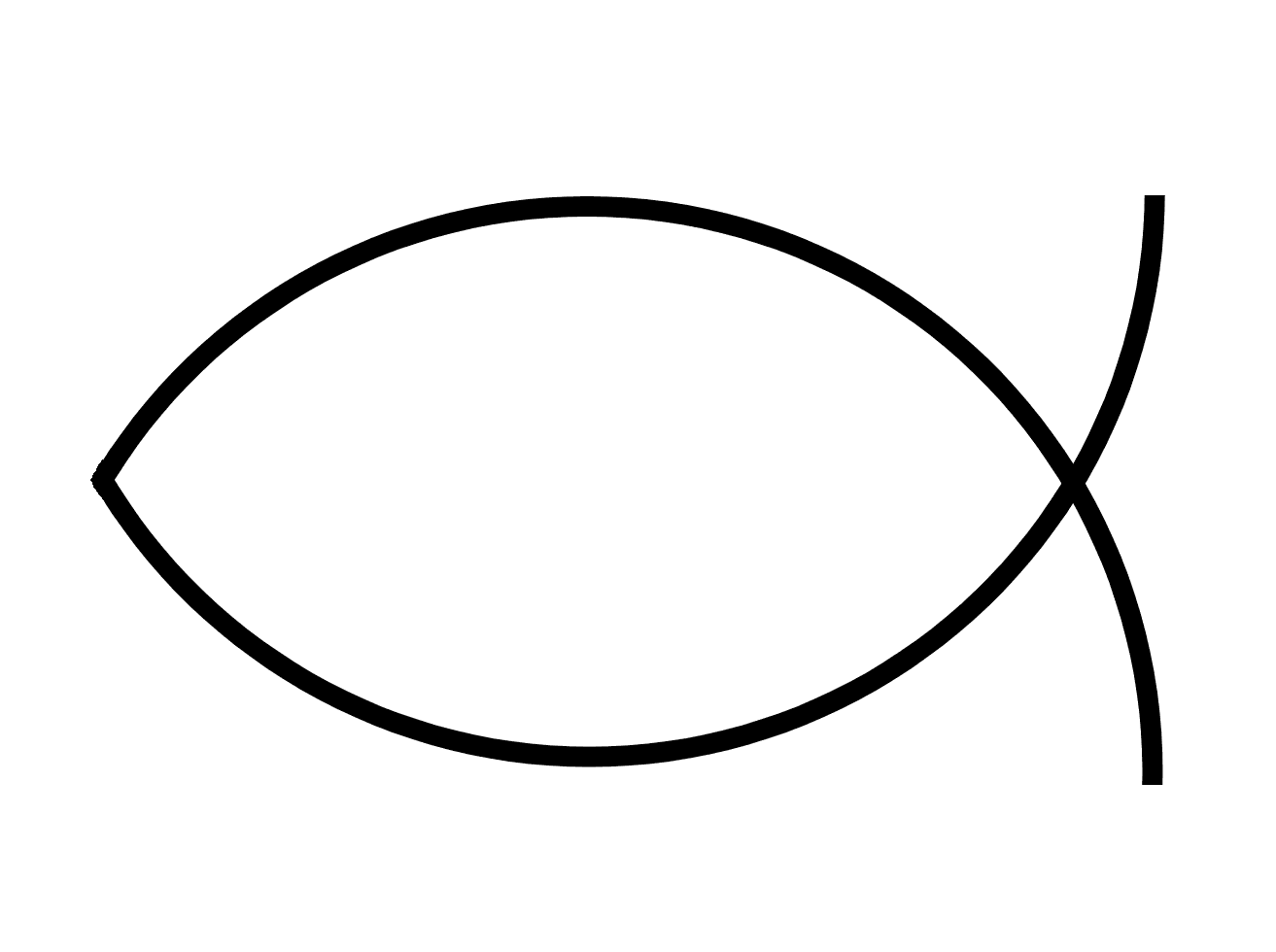
|
Vesica Pisces |
|
Christelijk symbool |
Heeft u bovenstaand symbool wel eens gezien? U ziet ze vaak als bumpersticker op auto’s, het symbool is het Ichtus-teken en het is waarschijnlijk afgeleid van de Vesica Pisces.
De Bijbel vertelt hoe God het licht schiep op de tweede dag. Welnu van de Vesica Pisces wordt nu, zoals we zullen uitleggen aan het einde van dit hoofdstuk aangenomen dat dit de geometrie is van de fotondeeltjestoestand van licht!
Gods schepping duurde zeven dagen en elke keer werd het centrum van een nieuwe bol geprojecteerd op het oppervlak van de vorige bol. Tel nu eens het aantal bollen in het genesispatroon, dan komen we uit op precies zeven, het exacte aantal dagen dat God nodig had om de wereld te scheppen volgens het eerst boek van de Bijbel, genaamd Genesis. Dit is ook de reden waarom bovenstaand patroon het genesispatroon genoemd wordt.
Wanneer we nu op dezelfde wijze doorgaan met Gods schepping maar dan iets langer dan de eerste 7 dagen, dan krijgen we de volgende figuur:
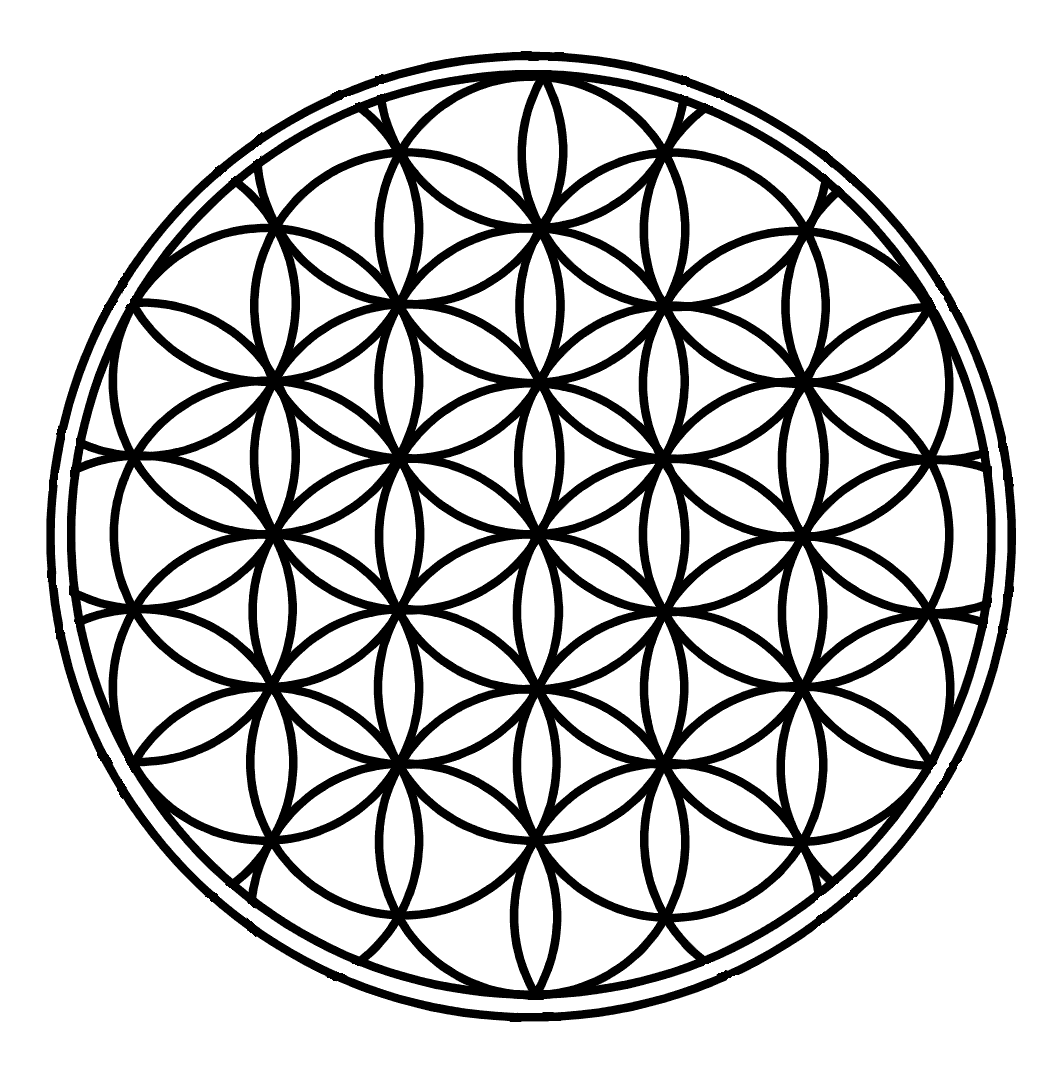
De Levensbloem
Deze figuur wordt de Levensbloem genoemd, merk de dubbele cirkels op die extra toegevoegd zijn aan de rand, deze figuur wordt over de hele wereld gevonden op oude gebouwen en heilige monumenten. Het is ook aangetroffen in tempels in Egypte. Er zijn nooit symbolen gevonden die het scheppingsverhaal uitbeelden voorbij het Levensbloempatroon en dit is waarschijnlijk ook de reden waarom de buitenste cirkels toegevoegd zijn. Op de een of andere manier wilde men in de Oudheid dit scheppingspatroon begrenzen tot de Levensbloem, misschien wel omdat er iets te verbergen viel?
Dus laten we eens vrolijk verder gaan met het creatiepatroon en kijken wat er nog meer verborgen ligt in dit patroon dat ontdekt werd door Drunvalo Melchizedek.
(2)
Laten we nog een volgende buitenste rand cirkels toevoegen. Wat we nu vinden wordt de Vrucht des Levens genoemd. Ik heb de bollen die de Vrucht des Levens vormen rood gekleurd om onderscheid te maken in het patroon, maar onthoudt dat wat we hier zien in werkelijkheid een driedimensionaal plaatje van bollen is.

|
|

|
De Vrucht des Levens |
|
|
Graancirkel, Wiltshire, 22 juli 2003 |
Welnu, de Vrucht des Levens wordt ook wel de vrouwelijke vorm genoemd omdat het enkel ronde vormen bezit net als de ronde vormen van het vrouwelijke lichaam. De mannelijke tegenhanger kan geconstrueerd worden door alle middelpunten van de bollen in dit plaatje middels rechte lijnen te verbinden. Het resultaat wordt de Kubus van Metatron genoemd.
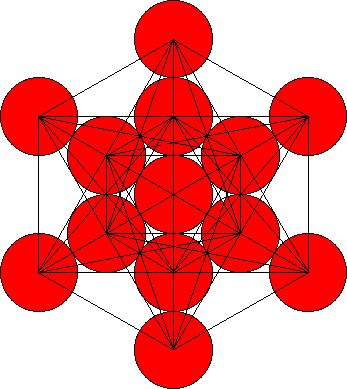
Kubus van Metatron
De Kubus van Metatron is erg belangrijk omdat het geometrische vormen bezit die een centrale rol spelen in de nieuwe etherfysica die we in het volgende hoofdstuk zullen bespreken.
De filosoof Plato beschreef al in 400 jaar v.Chr. de vormen die we vinden in de Kubus van Metatron en daarom worden ze ook wel de Platonische lichamen genoemd.
In feite vinden we de Platonische lichamen tweemaal terug in de Kubus van Metatron, een kleinere versie van de vormen wordt namelijk herhaald in de binnenste 7 bollen. Een van de bekendste Platonische lichamen is de kubus. Als u wilt, kunt u proberen deze te vinden in de Kubus van Metatron. Ik zal u een handje helpen:
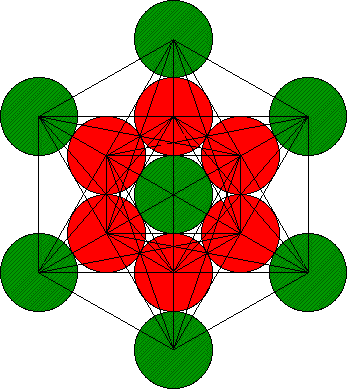
Kubus in de Kubus van Metatron
De groene bollen vormen de hoeken van de kubus. Er ontbreekt echter één bol die een hoek van de kubus vormt en aan het zicht onttrokken is.
Platonische lichamen
De vijf Platonische lichamen, genoemd naar de Griekse filosoof Plato, werden 350 jaar v.Chr. voor het eerst door Plato in zijn boek “Timaeus” beschreven. Hier zijn ze:
Tetraëder, Kubus, Octaëder, Dodecaëder en Icosaëder.

Graancirkel, West Overton, 24e juni 1999 octaëder geprojecteerd in 2D lay-out
Al deze vijf vormen zijn terug te vinden in de Kubus van Metatron, het kan even duren om ze te ontdekken maar ze zitten er allemaal in. De Platonische lichamen hebben zeer opmerkelijke eigenschappen, om te beginnen passen ze allemaal in een bol. De buitenste punten van de vormen liggen allemaal op het oppervlak van een omschrijvende cirkel. Ook passen alle vormen perfect in elkaar en kunnen perfect genest worden. Alle vormen hebben een tegenhanger, een tegengestelde vorm die gecreëerd kan worden uit de ander. De kubus bijvoorbeeld heeft de octaëder als tegenhanger. Als we de middelpunten van de vlakken van een kubus nemen en deze punten met elkaar verbinden d.m.v. lijnen dan ontstaat hieruit een octaëder. Hetzelfde proces kan omgedraaid worden om een kubus te creëren uit een octaëder. De tetraëder kent zichzelf als tegenhanger. De dodecaëder en de icosaëder zijn ook tegenhangers van elkaar. Elke lijn, vlak en hoek in een Platonisch lichaam zijn identiek aan elke andere lijn, vlak of hoek uit dezelfde vorm. Met andere woorden de Platonische lichamen zijn extreem symmetrisch.
Een ander verbazingwekkend symbool dat afgeleid is van de progressie van de Levensbloem, is de Levensboom. De Levensboom is een centraal onderwerp in de mystieke joodse Kabbala. De Levensboom kan over de Levensbloem heen gelegd worden en ze zullen naadloos over elkaar passen. De Levenboom is eigenlijk een extractie uit de Levensbloem waarbij de nodige bollen weggelaten zijn die er niet toe doen.

|
|

|
De Levensboom |
|
|
joodse Kabbala Levensboom |
In het volgende plaatje laten we zien dat de Levensboom perfect past over het genesissymbool. Begint u zo langzamerhand door te krijgen welke geometrische schoonheid en symmetrie verborgen liggen in al deze symbolen en hoe ze allemaal afkomstig zijn uit een progressie van het genesispatroon?

Levensboom over het Genesis patroon gelegd
De Levensboom is het mystieke symbool dat gebruikt wordt in de joodse Kabbala. De Levensboom wordt meerdere keren in de Bijbel genoemd als de boom die naast de boom van de kennis van goed en kwaad staat in de Hof van Eden.
Oude tradities vanuit de Oudheid vonden deze geometrische patronen erg belangrijk en hebben ervoor gezorgd dat ze bewaard bleven in mystieke esoterische wetenschappen.
Torus
De torus is ook een belangrijke geometrische driedimensionale vorm en we brengen hem hier ter sprake omdat de torus het bouwblok is van de materie in de nieuwe etherwetenschap van het volgende hoofdstuk. We kunnen de torus het beste vergeleken met een donut of de rookkring van een sigaar.
Hier is hij dan:

Torus
Het is eigenlijk een bol die van boven en onder naar binnen toe gekruld is, zodanig dat er een gat ontstaat in het midden. We kunnen de torus ook vergelijken met een appel. De torus ontstaat ook door het genesispatroon 360 graden te roteren om het middelpunt
Gulden Snede
Misschien wel het meest belangrijke onderwerp in de Heilige Geometrie is de Gulden snede. De Gulden snede is een speciale verhouding die wordt aangeduid met de Griekse letter Ф, Phi genaamd (spreek uit als fi).
Ze voldoet aan :
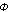 = ½ * v5 + ½
= 1.618 = ½ * v5 + ½
= 1.618
Phi is, net als het getal Pi, een irrationeel getal wat zoveel wil zeggen dat je haar waarde niet exact kunt berekenen, je kunt het alleen benaderen.
De Phi-ratio komt tot uitdrukking in de Gulden snede. De Gulden snede is de lengte van laten we zeggen een touw, wanneer dit zodanig in tweeën wordt gedeeld dat de verhouding van het langste gedeelte tot de gehele lengte gelijk is aan de verhouding van het kleinste deel van het touw tot het langste deel van het touw. (lees het nu nog eens!)
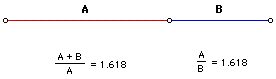
Wanneer de Phi-ratio toegepast wordt op een rechthoek waarvan zijde B = 1 en zijde A de lengte Ф heeft, dan spreken we van een Gulden rechthoek.
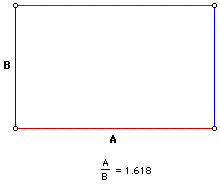
De Gulden rechthoek kan gebruikt worden om een spiraal te creëren, de Gulden Spiraal. Beginnend met een Gulden rechthoek kan er een tweede Gulden rechthoek tegen de eerste geplakt worden door gebruik te maken van de langste zijde A van de eerste rechthoek, die de kortste zijde B wordt van de volgende rechthoek. Om dit voor elkaar te krijgen moet de tweede rechthoek haaks op de eerste rechthoek geplaatst worden. Wanneer we dit proces voortzetten wat het “spiraliseren” van de Gulden rechthoek genoemd wordt, kan er een vloeiende lijn getrokken worden door de hoeken van alle rechthoeken zodanig dat de Gulden spiraal ontstaat. Het spiraliseren van de Gulden snede spiraal kan oneindig voortgezet worden in zowel binnenwaartse als buitenwaartse richting, ze wordt kleiner en kleiner wanneer ze inwaarts spiraliseert en groter en groter wanneer ze buitenwaarts spiraliseert.
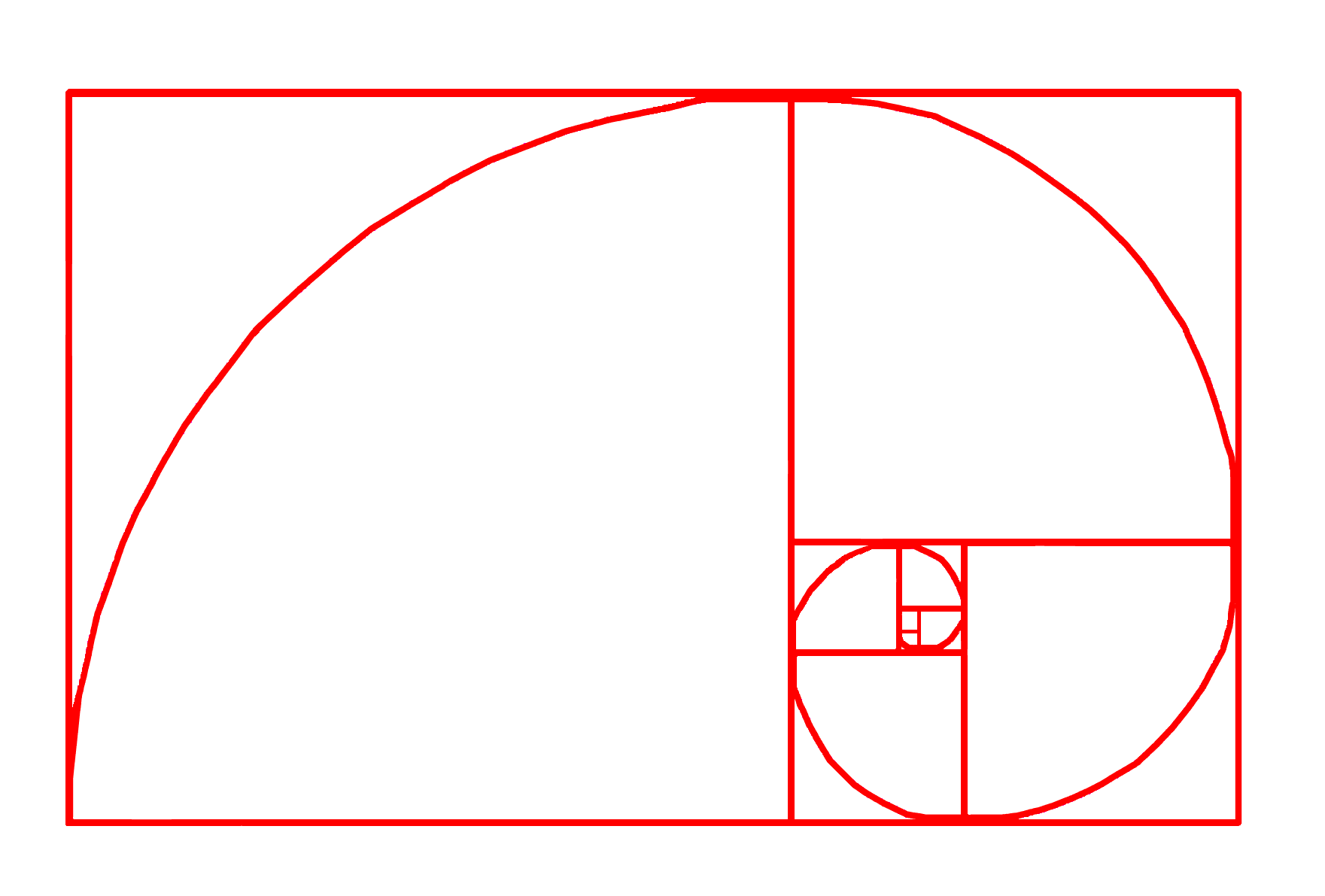
Gulden snede spiraal
Een variant van de Gulden snede spiraal is de Fibonacci-spiraal. Het verschil met de Gulden snede spiraal zit hem erin dat deze spiraal niet oneindig klein begint maar start met een Gulden rechthoek waarvan één zijde de lengte 1 heeft en de andere de lengte Phi. Geleidelijk aan, wanneer de Fibonacci-spiraal buitenwaarts spiraliseert, zal er nauwelijks nog verschil merkbaar zijn tussen de ware Gulden snede spiraal en de Fibonacci-spiraal.
De Fibonacci-spiraal is gebaseerd op de progressie van de Fibonacci-reeks.

Graancirkel, fractal spiralen, Milk Hill, Wiltshire 12 Augustus 2001
Fibonnaci reeks
Leonardo Fibonacci (1175 AD), een groot wiskundige uit de Middeleeuwen ontdekte de naar hem genoemde Fibonacci-reeks door de natuur te bestuderen. Doordat hij de groei van een konijnenpopulatie en de groei van bladeren en bloemblaadjes bestudeerde, ontdekte hij een bepaalde mathematische volgorde in deze groei:
Dit is de Fibonacci-reeks:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 etc.
Elke getal in de reeks is de som van de twee vorige getallen beginnend met het getal 1. De Fibonacci-reeks divergeert naar de Gulden snede wanneer we twee opeenvolgende getallen in de reeks op elkaar delen.
1/1 = 1
2/1 = 2,0
3/2 = 1,5
5/3 = 1,667
8/5 = 1,60
.
144/89 = 1,618
De Fibonacci-reeks divergeert dus naar Phi (Ф) maar bereikt haar nooit omdat het een irrationeel of transcendent getal is.
Fibonacci-spiralen en Gulden snede verhoudingen komen overal in het universum voor. De spiraal is de natuurlijke stromingsvorm van water wanneer het door het afvoerputje gaat. Het is ook de natuurlijke stromingsvorm van de lucht in tornado’s en orkanen. Hier is nog een mooi voorbeeld van een Fibonacci-spiraal in de natuur, de Nautilusschelp die in ieder boek over Heilige Geometrie voorkomt:

Nautilus schelp
De Gulden Snede komt talloze malen voor in het menselijke lichaam, in de verhoudingen van de botten en de lengte van armen en benen bijvoorbeeld. De Gulden Snede is ook de verhouding van de afstand van de navel tot de teen en van de navel tot de kruin. Michelangelo heeft deze Gulden Snede mooi verborgen in zijn fresco op het plafond van de Sixtijnse Kapel te Rome:
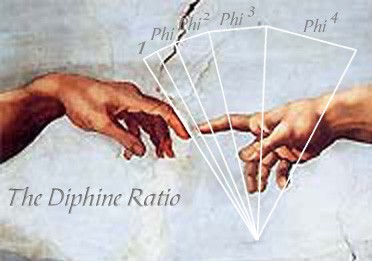
Michelangelo en de Phi-ratio’s in de menselijke hand
(Met dank aan Frank van den Bovenkamp, www.frankvandenbovenkamp.com)
Muziek
De Griekse filosoof Pythagoras ontdekte een wonderbaarlijke mathematische relatie tussen de harmonische noten in muziek. Het viel hem op dat door het indrukken van een snaar op verschillende posities op de fret van een gitaarachtig instrument er harmonische geluiden konden worden geproduceerd. Sommige noten klonken beter dan andere. Bij ieder indruk van een snaar werd de snaar in twee verschillende lengtes verdeeld en de verhouding tussen deze twee lengtes werd door Pythagoras gemeten. Hij schreef alle verhoudingen op die gezamenlijk harmonisch klonken. Op deze manier vond hij de volgende ratio’s:
1:1 (open snaar)
1:2 (ingedrukt op 1/3 van de lengte van de snaar)
3:2, 5:3, 13:8, 21:13, 34:21
Wat Pythagoras ontdekt had was de diatonische toonladder, zo genoemd vanwege het feit dat de snaar in twee lengtes verdeeld wordt (dia = twee). Deze verhoudingen corresponderen met de frequenties van de noten die voortgebracht worden door de witte toetsen van de piano wanneer deze gestemd staat in de diatonische toonladder. Na de 7e noot wordt het octaaf van 8 noten herhaald waarbij de eerste en de achtste noot verdubbelt in frequentie. De volgende zeven noten van de witte toetsen van de piano volgen weer precies dezelfde verhoudingen.
Welnu, wanneer u goed opgelet heeft dan is het u misschien al opgevallen dat de muzikale verhoudingen die ontdekt werden door Pythagoras overeenkomen met de verhoudingen uit de Fibonacci-reeks. Neem een willekeurig getal uit de Fibonacci-reeks en het daaropvolgende getal en je hebt de muzikale verhouding die ontdekt is door Pythagoras.
De Fibonacci-reeks is de reeks die ons mooie harmonischen geeft in de muziek. De diatonische toonladder is niet de enige toonladder, er zijn er nog veel meer en in werkelijkheid staat vandaag de dag ook geen enkele piano nog gestemd in de diatonische toonladder. Maar de principiële relatie tussen de harmonischen in de muziek en de mathematische progressie van de Fibonacci-reeks bestaat echt.
Stel je voor dat we een piano gestemd hebben in de diatonische toonladder en dat we het klavier van deze piano uitgebreid hebben met toetsen om in 49 octaven te voorzien! Dat zou een enorm grote piano worden waarvoor geen plek zou zijn in uw huiskamer! Maar stelt u zich voor dat we echt op zo’n piano zouden kunnen spelen. Wanneer we nu de noten in de laatste twee hoogste octaven, de toetsen die het verst aan de rechterkant van de piano liggen zouden bespelen, dan corresponderen de frequenties van deze noten met de kleuren van licht! Er komen zeven toetsen voor in deze hoogste octaaf en er zijn zeven primaire kleuren in het spectrum van licht, de zeven kleuren van de regenboog!
Dus de Fibonacci-reeks bepaalt niet alleen de verhoudingen van de harmonischen van het geluid maar ook die van het elektromagnetische spectrum van licht, het definieert de zeven kleuren van de regenboog!

Muziek en kleur, dezelfde harmonische ratio’s
We weten ondertussen dat veel musici zoals Beethoven, Mozart, Chopin, Bartók, Shubert en Debussy de Fibonacci-reeks en de Gulden snede opzettelijk gebruikt hebben, niet zozeer in de noten van het stuk, maar in de compositie zelf.
Beethoven gebruikte de Gulden snede in zijn beroemde Vijfde Symfonie. Zijn beroemde openingsmotto komt niet alleen in de eerst en de laatste maat van de symfonie voor, maar ook in de maat die precies de Gulden snede vormt van deze symfonie. Bela Bartók gebruikte de Gulden snede en de Fibonacci-reeks bewust in zijn composities in de maten 5, 8, 13, 21, 34, 55 en 89 waarin hij nieuwe instrumenten introduceerde zoals strijkers, cello’s en percussie-instrumenten. De vraag is dan ook waarom voegden deze componisten Heilige Geometrie toe aan hun muziek? Misschien waren ze niet alleen musici maar ook vrijmetselaars?
Kwadratuur van de cirkel

Een klassiek wiskundig probleem dat stamt uit de tijd van Plato wordt ook wel de ‘kwadratuur van de cirkel’ genoemd. In de laatste driehonderd jaar hebben wiskundigen tevergeefs geprobeerd met een oplossing te komen voor het probleem om met een passer en een winkelhaak een cirkel en een vierkant te construeren, zodanig dat beide dezelfde omtrek hebben. Pas in 1882 bewees Lindemann dat er helemaal geen oplossing bestaat voor dit probleem. Omdat Lindemann’s bewijs nogal complex is zullen we in simpele bewoordingen uitleggen waarom de cirkel niet vierkant gemaakt kan worden. De omtrek van een cirkel met een straal 1 is 2 * π en π (Pi) is een irrationeel getal (een transcendent getal, π kan nooit berekend worden, alleen benaderd).
Maar wanneer π irrationeel is en niet berekend kan worden, dan moet dit dus ook gelden voor de omtrek van de cirkel! De omtrek van het vierkant is echter een reëel getal omdat het vier maal de zijde van een vierkant bedraagt, hetgeen een reëel getal is dat gemeten kan worden. Dientengevolge kunnen de omtrek van cirkel en het vierkant in mathematische zin nooit gelijk zijn, ze kunnen hoogstens oneindig dicht bij elkaar liggen.
De Man van Vitruvius
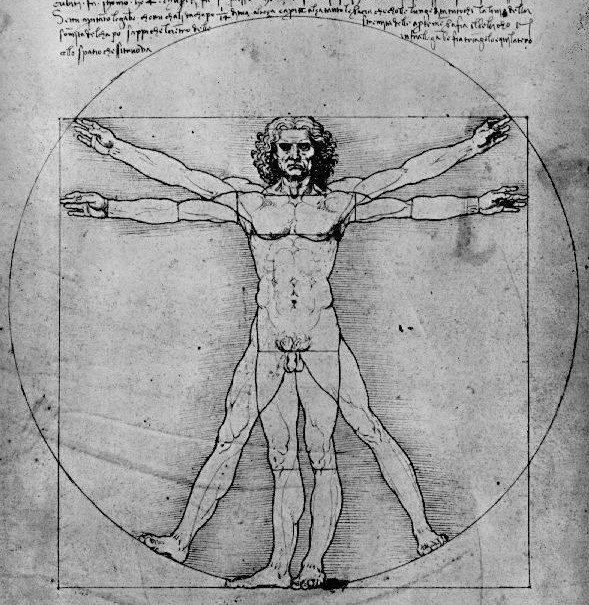
De Man van Vitruvius van Leonardo Da Vinci
Zie hier een interessante tekening van Leonardo Da Vinci. Wat hij laat zien in deze sketch is dat het menselijke lichaam de cirkel lijkt te kwadrateren. Wanneer de man zijn armen uitstrekt en ze horizontaal houdt past hij precies in het vierkant. Maar wanneer hij zijn benen spreidt en zijn armen omhoog houdt zoals in de schets, dan wordt het lichaam van de man perfect omschreven door een cirkel. De omtrek van het vierkant ‘is gelijk’ aan die van de cirkel.
Er is alleen al over deze schets veel geschreven, hij bevat een heleboel verborgen geheime geometrie. We zullen hier niet op alle details ingaan, maar ik wil u sommige wel zeer opmerkelijke dingen laten zien. De oude wijsheid, de hermetische traditie, vertelt dat het menselijke lichaam beschouwd kan worden als de blauwdruk van het universum vanwege alle verhoudingen die in het lichaam gevonden worden. Dit zou wel eens waar kunnen zijn. Laten we eens een kijkje nemen op het volgende plaatje:
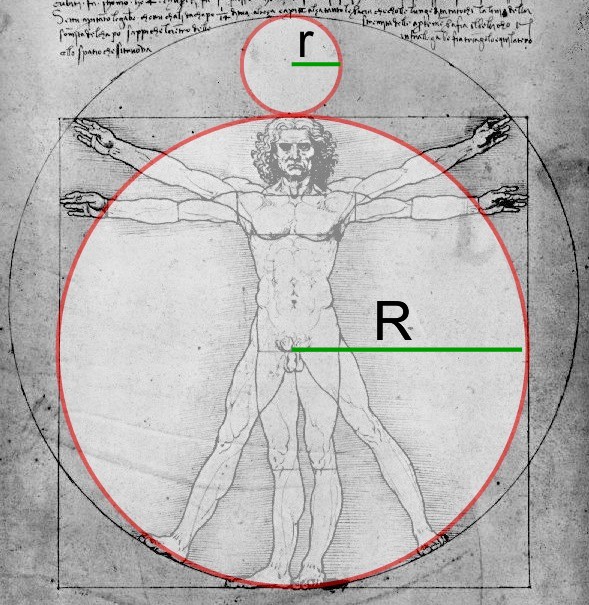
Het is hetzelfde plaatje als hierboven alleen zijn er nu twee rode cirkels aan toegevoegd. De grootste rode cirkel wordt omschreven door het vierkant. De kleinere rode cirkel ligt tussen de buitenste en de binnenste rode cirkel en raakt beide tangentiaal.
Tot onze verbazing stelt de bovenste rode cirkel de maan voor en de onderste rode cirkel de aarde! In mathematische termen: de verhouding van de straal van de kleine rode cirkel (r) t.o.v. die van de grote rode cirkel (R) is gelijk aan de verhouding van de diameter van de maan t.o.v. de diameter van de aarde. Wel laten we dit dan maar eens bewijzen:
(3)
Straal van de maan : r
Straal van de aarde : R
Zijde van het vierkant is : 2R
De omtrek van het vierkant is : 8 R
Straal van de buitenste cirkel is : r + R
De omtrek van de buitenste cirkel is : 2 π ( r + R )
Nu ‘kwadrateren we de cirkel’ ofwel we stellen de omtrek van de cirkel gelijk aan de omtrek van het vierkant:
8 R = 2 p ( r + R ) 
8 R - 2 p R = 2 p r 
R (8 – 2 p) = 2 p r 
r / R = (8 – 2 p) / 2 p = (4 – p) /
p
Straal van de aarde = 6,370,973 m
Straal van de maan = 1,738,000 m
Maan/aarde verhouding = r / R = 0.27279977
r / R = (4 – π) / π = 0.273239544 (π = 3.14159265)
Quod Erat Demonstrandum!
Er valt nog een mysterieuze relatie te ontdekken in de schets van de Man van Vitruvius van Leonardo Da Vinci. De Grote Piramide van Gizeh in Egypte genoemd naar farao Khufu (Cheops in het Grieks) die er begraven zou liggen, onderhoudt een perfecte relatie met de kwadratuur van de cirkel en de afbeelding van de Man van Vitruvius van Leonardo Da Vinci!
Kijk maar eens naar dit plaatje:
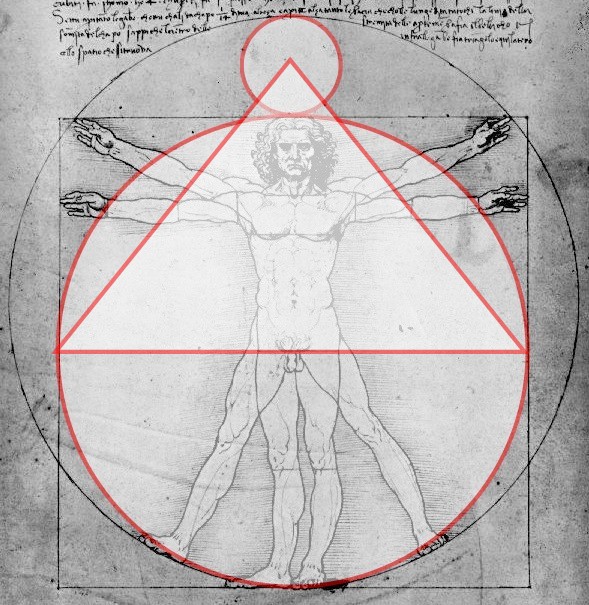
Grote Piramide van Gizeh in relatie tot de Man van Vitruvius
De driehoek in dit plaatje is namelijk de exacte geometrische verhouding van de Grote Piramide op het plateau van Gizeh nabij Caïro, Egypte. De hoeken tussen de basis en de top van de piramide is precies 51 graden en 51 seconden. (51º 51’).
(4)
De Grote Piramide en in feite de gehele lay-out van het plateau van Gizeh met al zijn piramiden, heilige tempels en de sfinx bevatten een heleboel Heilige Geometrie waarvan we meer zullen zien in dit boek. Het punt dat ik hier wil maken is dat de Egyptenaren op de hoogte waren van de kunst van de Heilige Geometrie en hoe deze zich verhoudt tot het universum, zoals het plateau van Gizeh en in het bijzonder de Grote Piramide.
En er was licht
Toen we het genesispatroon van de Heilige Geometrie bespraken, vermeldden we dat op de tweede dag van de schepping God de Vesica Pisces gecreëerd had, en dat de Vesica Pisces de geometrie is van het lichtdeeltje, de foton. De Bijbel vermeldt de tweede dag van de schepping als de schepping van het licht. Is het u overigens ook opgevallen dat de Vesica Pisces de vorm van een oog heeft?
Buckminster Fuller, die veel baanbrekend werk gedaan heeft in het herstellen van de Heilige Geometrie, ontdekte dat de geometrie van de foton overeenkomt met twee tetraëders die tegen elkaar aangeplakt moeten zijn.
Het blijkt dat de geometrische vorm van de dubbele tetraëder perfect ingesloten wordt door de Vesica Pisces waarbij de uitstekende punten van de tetraëder precies het vlak van de Vesica Pisces raken. Dit is tevens bevestigd door een andere bekende deskundige op het gebied van Heilige Geometrie, Drunvalo Melchizedek.
(5)
In de elektromagnetische golf (golfvorm van licht) vinden we de tetraëder ook terug als een verborgen geometrie. De elektrische en magnetische velden staan namelijk loodrecht op elkaar waardoor er een spiraal geconstrueerd kan worden precies over deze elektrische en magnetische velden heen. Deze spiraal loopt over een tetraëder.
Tom Bearden, de uitvinder van de MEG machine, heeft het bewijs gevonden dat ook James Clerk Maxwell dit geweten moet hebben maar dat Oliver Heaviside deze kennis van de verborgen tetraëder verwijderd heeft uit de vereenvoudigde versie van de elektrodynamica.
(6)
Notre-Dame van Chartres
De kennis van de Heilige Geometrie is bewaard gebleven in de architectuur van veel kerken en kathedralen in Europa. Zo is de kathedraal van Chartres beroemd vanwege de Heilige Geometrie die toegepast is in haar ontwerp. We vinden deze Heilige Geometrie bijvoorbeeld terug in de lay-out van het grondplan en in de glas-in-lood ramen waarin de Phi-ratio voorkomt.

|
|

|
Kathedraal van Chartres met grondplan |
|
|
|
|
In de vloer van het gotische schip van de kathedraal vinden we een raadselachtig labyrint, gemaakt uit witte steen en gezet in zwart marmer. Het labyrint meet vrijwel exact een tiende van de binnenmaat van de kathedraal en vormt een centraal punt, het brandpunt van de hele geometrische constructie van de kathedraal zelf. Het mag dus duidelijk zijn dat de ontwerpers dit punt wel heel bijzonder vonden.
De diameter van het labyrint heeft exact de grootte van het westelijke ronde raam dat in bovenstaande foto is afgebeeld. Daar komt bij dat de afstand van het centrum van dit raam tot aan de vloer dezelfde afstand is als die van het centrum van het labyrint tot aan de westelijke muur, de ingang van de kathedraal. Met andere woorden het westelijke ronde raam en het labyrint vormen een perfecte gelijkbenige driehoek.

Labyrint op de vloer in het schip
Ik heb persoonlijk het genoegen gehad om de kathedraal van Chartres een paar maal te bezoeken. Bij mijn laatste bezoek in de zomer van 2004 merkte ik een jong stel op, een jongen en een meisje. Het meisje knielde neer in het centrum van het labyrint en ging in meditatie waarbij ze haar handen hoog in de lucht hield. De jongen ging naast haar zitten. Terwijl ze toch flink veel aandacht trokken, leek het stel zich in het geheel niets aan te trekken van de passerende menigte. Ik was meteen geboeid. Het was duidelijk dat het stel meer moest weten over de heiligheid van dit labyrint gezien het feit dat ze deze plaats uitgekozen hadden voor hun meditatie. Maar wat had het in hemelsnaam te betekenen?
Wanneer we door het labyrint heen meanderen dan moeten we om beurten linker en rechter bochten maken. Daarbij verplaatsen we ons afwisselend naar binnen en naar buiten totdat we het centrum bereikt hebben. Volgens Daniel Winter, wiens fysica we nog zullen bestuderen in het volgende hoofdstuk, stelt dit labyrint de tweedimensionale symbolische projectie voor van Phi-spiralen die de torus vormen. De torus, zo wordt in zijn etherfysica aangenomen, is het bouwblok van het atoom en dus van de materie. Het labyrint is dan ook volgens Winter een symbolische projectie van de draaiende bochten die de Ph-spiralen van licht volgen op weg naar het centrum van het atoom.
De kathedraal van Chartres herbergt in het geheim kennis van de Heilige Geometrie, maar het heeft vele eeuwen geduurd voordat dit werd ontdekt. Heilige Geometrie werd niet alleen in de kathedraal van Chartres toegepast, maar in veel meer kathedralen en kerken in heel Frankrijk zoals in de kerken van Reims, Sens, Arras, Amiens, St Quentin, Bayeux en Toulouse om er maar een paar te noemen. Al deze kerken bezitten een labyrint gelijkend op dat van Chartres. Het moge duidelijk zijn dat het labyrint erg belangrijk was.
Frankrijk was het thuisland van de Merovingse koningen, een bloedlijn waarvan wordt aangenomen dat deze nazaten waren van Jezus Christus. Vele schrijvers beweren nu dat Jezus kinderen had bij Maria Magdelena en dat de katholieke kerk dit feit voor eeuwen geheim heeft weten te houden. Het idee heeft veel publieke aandacht kregen sinds het boek de ‘Da Vinci Code’ van Dan Brown dat gepubliceerd werd in de zomer van 2004. De nazaten van Jezus vormen de bloedlijn van de Heilige Graal. Sporen van deze bloedlijn leiden naar Rennes Le Chateau in Frankrijk en Roswell Chapel in Groot-Britannië, het thuisland van de Tempeliers en Koning Arthur. Het geheim van het huwelijk van Jezus en Maria Magdelena en hun nageslacht werd eeuwenlang veilig bewaard in geheime genootschappen.
Naar nu wordt aangenomen, bewaarden deze geheime genootschappen ook wetenschappelijk en gnostische kennis waarvan de sporen terug te voeren zijn tot het mythologische Atlantis. Atlantische kennis, zo wordt vermoed, is doorgegeven aan de Egyptenaren en van de Egyptenaren naar de Griekse hermetische traditie. In onze moderne tijd is het bewaard gebleven in de vrijmetselarij die door de eeuwen bestaan heeft. Leonardo Da Vinci was lid van zo’n kring die hem toegang verschafte tot de wetenschap van de Heilige Geometrie en zijn lidmaatschap verklaart dus waarom hij het toepaste in zijn schilderijen. Het belang van de Heilige Geometrie, in het bijzonder de betekenis van de Gulden snede is toegepast in vele kunstvormen in de moderne geschiedenis, van de schilderijen van Leonardo Da Vinci tot de architectuur van kerken en kathedralen evenals in de muziek zoals in de Vijfde van Beethoven.
(7)
Recapitulatie
Dit hoofdstuk was een les in de Heilige Geometrie. Ik zou het niet in dit boek geïntroduceerd hebben, ware het niet dat het zo’n belangrijke rol speelt in een nieuwe fysica die vorm begint te krijgen. Wetenschappers zijn de betekenis van geometrische en fractalpatronen aan het ontdekken in ons fysieke universum, zoals in de gravitatie en elektromagnetische velden van de aarde, de structuur van het atoom en het energieveld van het menselijke lichaam.
In hoofdstuk 3 hebben we aangetoond dat de scheiding tussen de fysieke en mentale dimensies zoals die is voorgesteld door René Descartes in werkelijkheid niet bestaat. De kracht van de menselijke geest is enorm onderschat en bezit vermogens van geest boven de materie. Kwantumfysicus Amit Goswami stelt dat bewustzijn oorspronkelijk is en dat hieruit de fysieke wereld gecreëerd wordt.
In hoofdstuk 4 hebben we het nulpuntsveld besproken dat ontdekt is door de kwantumfysica. Het nulpuntsveld is een ongelimiteerd en onuitputtelijk energieveld dat aanwezig is in het gehele universum. We suggereerden al dat nulpuntsenergie wel eens een spirituele energie zou kunnen zijn die Amit Goswami’s beweringen zou kunnen staven.
In dit hoofdstuk hebben we verder de Heilige Geometrie bestudeerd, een oude wetenschap die herontdekt is door hedendaagse wetenschappers.
In het volgende hoofdstuk zullen we de Heilige Geometrie, het nulpuntsveld en de nieuwe inzichten in bewustzijn gebruiken om te laten zien hoe wetenschappers deze samenvoegen in een nieuw fysisch model, een theorie van alles, die zowel het fysieke als het mentale domein verklaart. We zullen ook zien hoe de hedendaagse wetenschap herontdekt wat Plato 2350 jaar geleden al opperde, namelijk dat de wereld van het atoom is opgebouwd uit Platonische lichamen. Tevens zullen we de rol en betekenis van de Gulden snede in golfvormen onderzoeken.
|